 |
| 直線在正投影平面上的圖形 |
 |
| 直線在正投影平面上的圖形 |
 |
| 直線在正投影平面上的圖形 |
在正投影平面上的圖形都是實長
與 X-Y 平面平行的平面, 在平面上所畫的圖形, 都是實長.
如前視圖, 軸線外的三條水平青色線, 其上視圖, 即青色圖形.
圖中的立方體, 有六個面, 可以想像成正投影中的正投影面.
在各個面上所畫的圖形, 都是實長.
如圖中的紅, 黃, 綠, 青, 洋紅線段.
在立方體中找線段的實長
輔助投影視圖畫實長:
圖中的 AC線段, 在正投影的三個視圖, 都是一條斜線.
所以, 三條斜線都不是實長.
這個範例, 是作輔助視圖來畫出線段 AC 的實長.
這裡是在上視圖的 AC 向外平行做輔視圖.
也可以在前視圖或右視圖做輔視圖.
首先, 將上視圖中的 AC 線段 ( 長 250 ),
向左上方偏移到圖形外的適當位置,
即平行 AC 的線段 AD
( 長度 = 250, 也是前視圖中 AD 的實長 ).
然後, 再將線段 AD, 向外偏移 100 ( 前視圖中的高度 ), 就得到線段 BC, 畫AC黃色線段, 就是實長 269.3 mm.
輔助視圖, 就是建立 ABCD 這個輔助的投影面, 來畫出線段 AC 的實長.
由上視圖畫輔助視圖, 必須由相鄰的正投影視圖取高度.
此例相鄰的視圖為前視圖.
如果, 要從右視圖取高度, 也是可以.
初學者最好先將右視圖逆時鐘旋轉90度, 相對應放在上視圖的右邊.
這樣, 只看這兩個圖, 可視為另一型式的前視圖和右視圖.
由前視圖做輔助視圖, 從右視圖取高度 100 ( CD 線長 ).
這次由正視圖剖切黃色線, 並且向右下方做輔助投影面, 求實長.
找實長的方法相似, 是在正視圖中的黃色線上做一輔助投影面, 由上視圖看, 這一刀, 即 ABCD 這個矩形. 如果很難理解, 可以同時比對立體圖中的相對位置.
上視圖中的 BC 為水平, 所以正視圖中的 BC 為實長 180.3; 正視圖中, AB 同點, 所以上視圖 AB 為實長 200.
在輔助投影圖中, AD 向右下偏移 200, 為紅色線BC. 連接對角線 AC, 即得黃色線段, 實長 269.3
因為是在前視圖中做輔助視圖, 而上視圖或右視圖都與前視圖相鄰.
所以, 可以任取上視圖或右視圖的高度值來畫輔助視圖, 結果都會相同.
如果, 畫實長過程常卡住, 不知下一步該怎麼做. 可以學這裡的小技巧, 在三視圖和立體圖中, 標示 A, B, C, D,…等正確的點位, 會比較容易讀圖.
另一種求實長的畫法, 是將黃色線段一端固定, 另一端旋轉到垂直/水平線, 也就是相鄰視圖的投影面上.
在上視圖中, 黃色線段 AB 的 A 端固定 ( 正視圖中, 是黃色線段OB 的 O 端 ), 以 A 點為圓心, 250mm 為半徑往正視圖方向畫圓弧, 到上視圖中的 C點, 向下投影到正視圖中的C點. 連接成洋紅色線段 OC, 長度 269.3 即為黃色線段的實長.
如果, 三視圖實長的畫法不好理解, 可以看右上角的立體圖示.
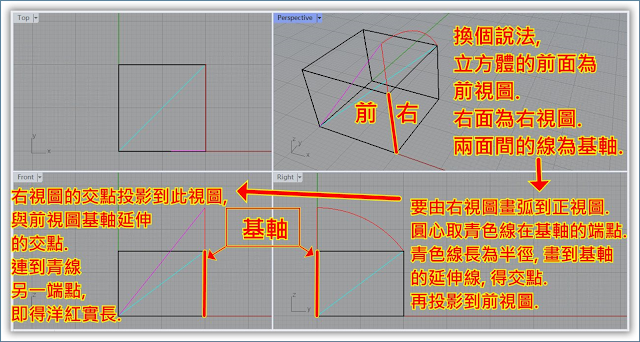
黃色線段取O點固定不動, 以OA為軸心, 另一端點B在上視圖的平面上, 以紅色線段長 AB 為半徑, 往前視圖方向畫圓弧, 交到上視圖的C點, 前視圖中的 OC 洋紅色線段即為正視投影面上的實長. 黃色線段以OA為軸心, 由 AB 轉到 AC, 正投影面上的 OC 為實長.
左上方的立體圖, 展示由上視圖畫弧到前視圖中畫出實長.
右上方的立體圖, 則展示由右視圖畫弧往前視圖中, 畫出實長線段.
兩者取的視圖不同, 但結果都一致, 畫出線長 269.3 的線段 OC.
如果, 您能從三個正投影視圖中的兩個視圖, 逐步畫出實長, 且結果相同. 基礎觀念就已經建立, 正確了.
這圖已經包含正投影三視圖畫法, 輔助圖畫法, 線段在三視圖的端點位置, 文字輔助識圖的技巧.
在實際圖面上, 黃色線的周圍, 會有很多圖形, 線條, 文字, 標註. 需要些技巧來快速找到它.
在立體圖中, 正圓錐體上的素線 ( 底圓上取任意點, 到圓錐頂點所連成的線段 ) , 可以清楚, 直覺的理解為實長.
這個圖, 圓錐倒著畫. 可以嘗試畫出實長.
圓管, 圓管切一刀, 大小頭, 四角轉圓,…的展開, 都可以用實長的概念畫展開.
正投影實長找法:
- 投影面中, 一線的端點, 在相鄰視圖為水平或垂直線, 這條水平或垂直線就是實長.
- 投影面中的線為水平或垂直線, 相鄰視圖中, 相對端點所看到的斜線, 就是實長.
- 所有投影面中, 看到的都是斜線, 這條線為複斜線. 所有視圖所看到的, 都只是它在各投影視圖中的投影, 非實長.
四個角點看起來像共平面.
但右視圖中, 左上角兩點重疊, 表示左視圖上水平線為實長.
右下角的邊線為垂直線,表示左視圖的斜線為實長.
回到右視圖來看,
左上角點處是一垂直向的正投影面,
而右下角的垂直線並不在這個投影面上.
所以左圖中的四角點不共平面.
左圖的上水平線和右下斜線是實長, 所以這兩條線是明確的.
由右圖左邊, 下面垂直線的兩端, 都接到左上角的同一點, 形成一個三角形.
所以, 這個三角形, 在左圖, 就是由右下斜線的左下端點, 畫到上水平線的右端點, 再回到斜線的右上端點.
一般彎頭的平面畫法, 因為是畫平面圖形, 都會畫成類似上圖的圖形.
看起來很順, 哪裡有問題嗎?
彎頭的重點, 兩端面一定是圓管直徑-正圓.
兩端為半魚, 中間為全魚,
這樣, 半魚的斜切端面和全魚的兩側端面才會相同-橢圓形.
如果, 用端面夾角來判斷,
則全魚夾角一定是半魚斜切端面側夾角的兩倍.
以上圖為例,
總夾角 22 度, 分3段,
即一全兩半,
可視做2全.
22/2=11,
全的端面夾角要做 11 度,
半的夾角 5.5 度才正確.